Über das Buch

Inhalt

Beispiel einer rechten und linken Seite (hier: Parabelgleichung aufstellen; immer die rechte Theorie-Seite zuerst anschauen, dann das Bsp. links - und schon ist alles klar)

Weiteres Bsp.: Parabelgleichung mittels der Scheitelspunktsform aufstellen (zuerst rechts)

Aufg. zum Kosinus-Satz und Sinus-Satz

Lösung zur Aufg. mit Kosinus-Satz

a² = 4,5² + 3,8² - 2*4,5*3,8*cos78°

a² = 34,69 – 34,2*cos78°

a² = 34,69 – 7,11

a² = 27,58

a = 5,25 km

Bitte auf Zeichnung klicken.Für sin usw im rechtw. Dreieck; Sinus- und Kosinus-Satz.

Geg.: Länge der Strecke [AB] = 381,94 m. Von B aus sieht man die Spitze unter dem Winkel von 22°.

Von A aus sieht man die Spitze unter dem Winkel von 34°.

Gesucht: Höhe des Eiffelturms; Länge der Strecke [AS] und wie weit ist A vom ersten Fuß des Turmes (P selbst beschriften) entfernt. Länge der Strecke [SB] berechnen. Alles nur zur Übung und weil es im Ernstfall dafür Punkte gibt. Die Winkel in Blau = Hinweise.

Tipp: immer dran denken, wenn es um eine Höhe geht, ist am Boden garantiert ein rechter Winkel !

Denke daran, du kommst schon lange nicht mehr mit einem Ansatz zur Lösung. Es schadet auch nicht, sich an die 7. Klasse zu erinnern. Dort hat man ne Menge über Winkel gelernt.

Auf einem Berg steht ein 16 m hoher Tempel. Der Fußpunkt A vom Tempel und dessen höchster Punkt B können von einem Punkt C in der Ebene unter den Höhenwinkel α = 32,3° und β = 35,2° gesehen werden. Wie hoch ist der Berg?

Rotationskörper

Wirklich das Einzige, was hier schiefgehen kann ist, dass ihr das Volumen berechnet und leider war die Oberfläche gesucht. Oder umgekehrt: Oberfläche wird fein berechnet, gesucht war allerdings das Volumen.
Deshalb ganz wichtig: Schlüsselwörter (Volumen oder Flächen) im Text mit gelb markieren und nochmals rausschreiben.
Ich habs leider schon oft gesehen: ganze Seite mit 1000 Flächenberechnungen, alles richtig, trotzdem Null Punkte, da Volumen gesucht war.

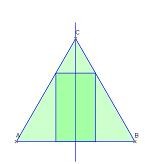
Axialschnitt eines Kegels mit einbeschriebenem Zylinder

5.0 Einem geraden Kreiskegel, dessen Axialschnitt ein gleichseitiges Dreieck mit 12 cm Seitenlänge ist, werden gerade Kreiszylinder einbeschrieben.
Dabei liegen die Grundflächenkreise der Zylinder und des Kegels aufeinander.
Für den Grundkreisradius r der einbeschriebenen Zylinder gilt:

r = x cm mit x aus ] 0 ; 6 [ .

5.1 Zeichnen Sie einen Axialschnitt des Kegels und die zu x = 2 und x = 4,5 gehörenden einbeschriebenen Zylinder.

5.2 Zeigen Sie, dass für die Höhe hz der einbeschriebenen Zylinder in Abhängigkeit von x gilt:
hz = Wurzel aus 3 * (6-x) cm. Tipp: zuerst CM (mit Strich drüber) berechnen. M ist Mittelpunkt von AB (auch als Strecke geschrieben, also mit Strich drüber). Bitte den Wurzelterm stehenlassen! CM = 6 * Wurzel 3 Dann Skizze nur Dreieck MBC mit einem Rechteck drin und dann geschickt den 4-Strecken-Satz.

5.3 Berechnen Sie, zu welchem Wert von x ein Zylinder gehört, bei dem der Durchmesser des Grundkreises so lang wie seine Höhe ist. Tipp: Skizze und beschriften!
Runden Sie dabei auf zwei Stellen nach dem Komma.
[Teilergebnis: x = 2,78 cm]

5.4 Berechnen Sie den Inhalt der Mantelfläche für den Zylinder aus 5.3.

5.5 Zeigen Sie, dass sich die Mantelfläche der Zylinder allgemein folgendermaßen darstellen lässt:

Mz (x) = 2*pi*(Wurzel aus 3)*(6x-x²) cm².

5.6 Ermitteln Sie rechnerisch den Wert für x, so dass der zugehörige Zylinder eine möglichst große Mantelfläche besitzt.
Geben Sie auch den Wert der größten Mantelfläche an.
Runden Sie dabei auf zwei Stellen nach dem Komma.

Tipps

Punkte An wandern auf einer Parabel ( y = -0,5x² +3x + 0,5 ). Die Koordinaten sind dann immer:
An ( x | "Parabelgleichung" ). Natürlich nur der Rechtsterm, also An ( x | -0,5x² +3x + 0,5 ).

Mal angenommen, es gibt Punkte Cn mit Cn ( x + 2 | "Geradengleichung" ) , dann bedeutet dies:

der Punkt C1 liegt immer um 2 cm nach rechts bezüglich des Punktes A1. Die Cn wandern hier z. B. auf einer Geraden g: y = 0,5x - 4. Angenommen A1 liegt bei x = 1,5 , dann liegt C1 bei x = 3.5 (nur halt auf der Geraden. Klar?
Angenommen A2 liegt bei x = -1 (auf der Parabel), dann liegt C2 bei x = 1 (also 2 nach rechts auf der Geraden. Kommt immer wieder mal vor.

Um zu vergrößern, bitte einfach draufklicken.

Kleine Parabel-Aufgabe für 30 min.

Typische, einfache AP-Aufgabe (1.5 ist anspruchsvoll)

Lösung zu 1.4
x = 1,5

Lösung zu 1.6
x1 = -1,79 und x2 = 4,79

Hat jemand eine Lösungsidee zu 1.5 ?
Bitte ins Gästebuch schreiben oder Frage stellen.
Also hier mal ein Lösungshinweis:
Meine Rede ist immer: Beute die Information im Text brutal aus!!!
Bedeutet hier: Raute als Sonderfall der Drachenvierecke. Alle Eigenschaften markieren in Skizze oder rausschreiben - hoppla - da ist ja der Lösungsansatz.
Und nochmal: wer mit der 3 oder 4 in der Mathe-AP zufrieden ist, brauch diese Aufgaben nicht zu berühren. Das ist keine Arroganz, sondern eiskalte Strategie!!!!!

Rotations-Aufgabe A 3.0 Gegeben ist das gleichschenklige Dreieck ABC mit der Basislänge AB = 3 cm und dem Winkel ACB mit dem Maß 40°.

A 3.1 Zeichnen Sie das Dreieck ABC und seinen Inkreis mit dem Mittelpunkt M im Maßstab 3 : 1. (2 Punkte)

A 3.2 Der Punkt D ist der Mittelpunkt der Basis [AB]. Berechnen Sie auf zwei Stellen nach dem Komma gerundet die Höhe [DC], die Länge der Seite [AC] und den Inkreisradius r_i. [Ergebnisse: DC = 4,12 cm ; AC = 4,39 cm ; r_i = 1,05 cm] (3 Punkte)

A 3.3 Das gleichschenklige Dreieck ABC ist der Axialschnitt (Schnitt einer geometrischen Figur entlang seiner Achse, hier also ein Dreieck) eines Kegels, der die Grundform einer neuen Pralinensorte beschreibt. Im Inneren der Praline befindet sich eine Knusperkugel. Im Axialschnitt fällt der Mittelpunkt der Knusperkugel mit dem Inkreismittelpunkt M des Dreiecks ABC zusammen. Der Radius r_K der Knusperkugel ist um 1,5 mm kleiner als der Inkreisradius r_i. Berechnen Sie den prozentualen Anteil des Volumens der Knusperkugel am Gesamtvolumen der Praline. (Auf zwei Stellen nach dem Komma runden.) (4 P.)

A 3.4 Die Punkte p auf [AC] und Q auf [BC] sind jeweils 1,5 cm von der Pralinenspitze C entfernt. Ergänzen Sie die Zeichnung in 3.1 durch das Dreieck PQC und berechnen Sie die Länge der Strecke [PQ] auf zwei Stellen nach dem Komma gerundet. [Teilergebnis: PQ = 1,03 cm ] (2 P.)

A 3.5 Der obere Teil der Praline mit dem Axialschnitt PQC soll mit einer kreissektorförmigen Goldfolie vollständig bedeckt werden. Berechnen Sie das Mindestmaß w des Mittelpunktswinkels dieses Kreissektors auf zwei Stellen nach dem Komma gerundet. (1 P.)

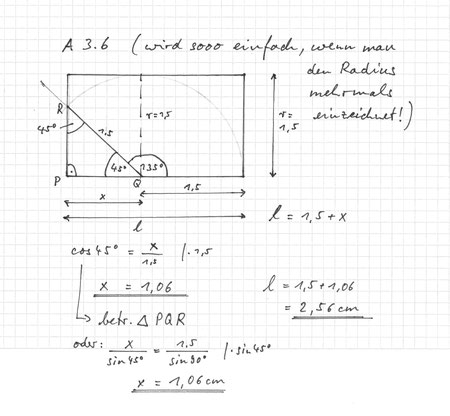
A 3.6 Zum Einwickeln des oberen Teils der Praline aus 3.5 wird aus einem rechteckigen Folienstück mit einer Breite von 1,5 cm ein Kreissektor herausgeschnitten (siehe Skizze, wird später nachgereicht). Aus praktischen Gründen wird dafür ein Mittelpunktswinkel mit dem Maß omega-stern = 135° gewählt.
Zeichnen Sie den Kreissektor und das zugehörige rechteckige Folienstück im Maßstab 3 : 1. Berechnen Sie sodann die Länge l dieses Folienstücks auf zwei Stellen nach dem Komma gerundet. (4 P.)

Ganz wichtig ist zunächst die Zeichnung als Schrägbild.

Weiteres folgt asap ...

Die Grundfläche der Pyramide ABCDS ist ein Drachenviereck

mit AC als Symmetrieachse. Die Spitze S liegt senkrecht über

dem Diagonalenschnittpunkt M und es gilt: (q=1/2 ; omega = 45°)

Länge der Strecke [AC] ist 10 cm. Länge der Strecke [AM] ist 3 cm.

Länge der Strecke [BD] ist 8 cm. Länge der Strecke [MS] ist 10 cm.

Berechne das Maß alpha des Winkels CAS und das Maß phi des Winkels BSD.

Hier noch einige Berechnungen zu den Kanten der Pyramide oben und zur Seitenberechnung.

weitere Ergebnisse zur Pyramiden Aufg.
alpha=73,30° phi=43,60° AB(immer mit Strich drüber)=5 cm
BC=6,40 cm AS=10,44 cm CS=11,18 cm BS=10,77 cm
<MBS=68,20° <ACS=63,43° <ASC=43,27° <CDS=76,59°
<SCD=69,56° <DSC=33,85° <ASB=27,21° <BAS=80,04°
<SBA=72,75° nicht alle Seiten und Winkel nötig, da Symmetrie.
Flächen über A1 = 0,5 * Seite * Seite * sin(eingeschl. <)
etc. echt ne Menge zum Üben - Routine aufbauen.

Letzter Punkt der Ex. Punkt Pn wandert

Zwei Orte A und B liegen in einer Horizontalebene 12,5 km voneinander entfernt. Ein Hubschrauber, der im geraden Horizontalflug über beide Orte direkt hinwegfliegt, wird gleichzeitig in A unter dem Höhenwinkel α₁ = 68,6° und in B unter dem Höhenwinkel
β₁ = 37,5° angepeilt. Nach t = 150 Sekunden wird eine zweite Peilung vorgenommen und bei A ist α₂ = 32,2° und bei B ist jetzt β₂ = 84,4°. In welcher Höhe und mit welcher Geschwindigkeit flog der Hubschrauber?

Abschlussprüfungen

AP 2010 und AP 2009